【目次|SPSSの使い方】へ

因子分析 (FACTOR)

【用途】因子分析【を開く】は、分析に投入した量的変数でおたがいに相関が強い変数の合成変量を因子として、その因子と個々の変数との関係を調べることを通じて、変数の分類を可能とする手法であり、1.事前に下位次元を設定した尺度を構成する指標間の内的一貫性および異なる下位次元の尺度間の独立性の検討や、2.ある変数群の潜在的次元の探索的分析のために行う。

【データ】【出力例1】では、國學院大学　経済ネットワーキング学科「社会経済調査�UA･B」　1999年度「企業の環境対策への取り組みと商品開発戦略についての調査」【を開く】の問８「貴社は商品開発を行ううえでどのような点を重視していますか」（回答選択肢は「ほとんど重視していない」に1点、「あまり重視していない」に2点、「かなり重視している」に3点、「非常に重視している」に4点を与える3点尺度）
　【出力例2】では、國學院大学　経済学部「アンケート調査」　2011年度「学食、スポーツ、インターネットの利用、ゲーム、自動車会社、行ってみたい国および収入と支出についての調査」【を開く】設問21 あなたが大学のコンピュータ教室以外でインターネットに接続するとき使用する機械を、つぎのなかからすべて選んでください（二値択一型多重回答方式設問）にどのような潜在的次元があるのか探索するための因子分析を行う。

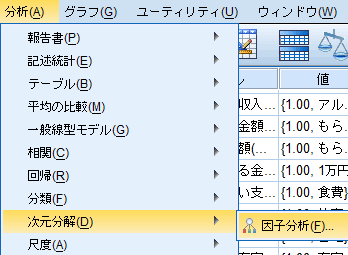
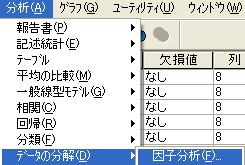
1. メイン・メニューの［分析］を選択し、ドロップダウン・リストから、16版以降では[次元分解]、15版以前では[データの分解]を、その右のドロップダウン・リストから[因子分析]を選択する(図1)。

   22版	15版
   図1　[次元分解]→[因子分析]の選択

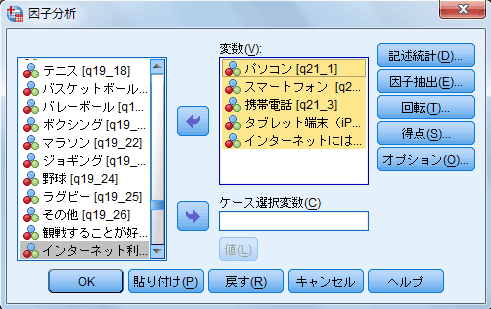
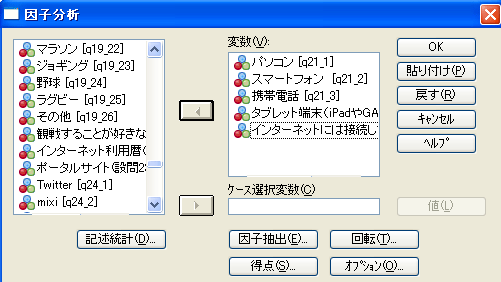
2. 左側の変数リストから分析に投入する変数を選択し、右向き（この図では変数を選択した後なので左向きになっているが）16版以降ならば矢印、15版以前ならば三角形のボタンをクリックすると、右側の変数ボックスに変数が表示される(図2)。

   22版	15版
   図2　[因子分析]ダイアログ・ボックス

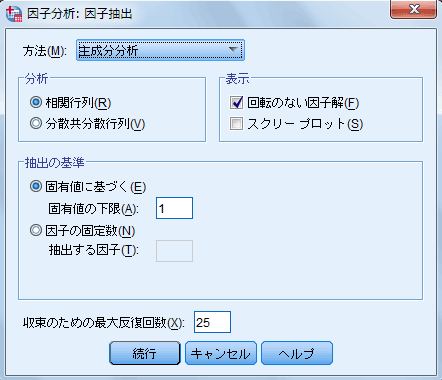
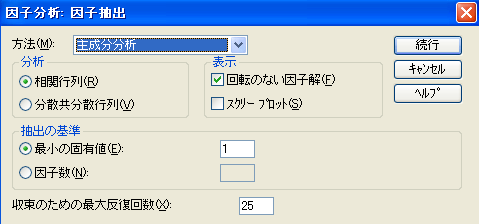
3. [因子抽出]ボタンをクリックすると、[因子分析:因子抽出]ダイアログ・ボックスが開かれる(図3)。因子抽出方法のデフォルトは主成分分析法であるが、主因子法などその他の抽出方法を選択するときには、[方法]ドロップダウン・リストから選択する。
4. デフォルトでは因子の抽出をうち切る基準は、固有値が１以上の因子までを抽出することであるが、これも変更することができる。

   22版	15版
   図3　[因子分析:因子抽出]ダイアログ・ボックス

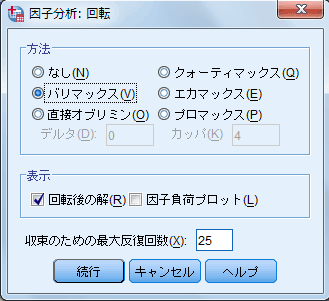
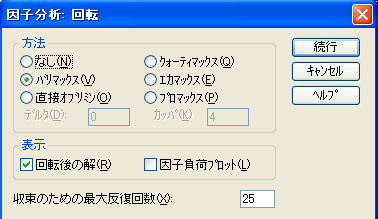
5. デフォルトでは「回転のない因子解」(回転前の因子負荷量行列)が出力されるが、（図２の因子分析ダイアログ・ボックスの）[回転]ボタンをクリックすると[因子分析:回転]ダイアログ・ボックスが開かれる。
6. 分析に投入した１つの変数が１つの因子だけに因子負荷量が強くなるようにするためには、因子負荷行列の回転を行う。通常はバリマックス回転を選択する。なお、（狭義の因子分析ではない）主成分分析を行う場合にはデフォルトの[回転のない因子解]を選択する。

   22版	15版
   図4　[因子分析:回転]ダイアログ・ボックス

7. 「1変量の記述統計量」(有効ケース数、平均値、標準偏差)、相関係数などの記述統計が必要な場合には、図2の[記述統計]ボタンをクリックする。
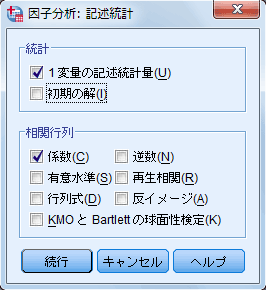
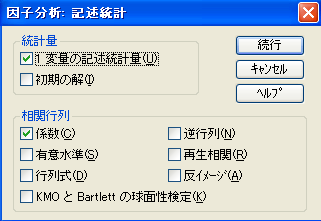
8. [因子分析:記述統計]ダイアログ・ボックス(図5)が開かれるので、必要な統計量をチェックする。

   22版	15版
   図5　[因子分析:記述統計]ダイアログ・ボックス

9. 各ダイアログ・ボックスの[続行]ボタンをクリックして[因子分析]ダイアログ・ボックスに戻り[OK]ボタンをクリックする。

【デフォルトの出力】共通性（初期値と因子抽出後）、説明された分散の合計、成分（因子負荷量）行列（浮動小数点表示）、成分変換行列

【出力例1：1999年度　問８　商品開発を行ううえで重視している点の因子分析】
　

共通性   初期 因子抽出後 価格 1.000 .610 デザイン 1.000 .810 ネーミング 1.000 .793 顧客ニーズ 1.000 .390 費用 1.000 .509 アフターフォロー 1.000 .431 因子抽出法: 主成分分析

　デフォルトの出力である表3の説明された分散の合計は、実質的には固有値と分散の説明率である。（SPSS　22版でも）「因子」を「成分」、「固有値」を「合計」と誤表示している。図3で変更できるが、因子抽出の打ち切り基準を固有値の下限=1というデフォルトの設定で、固有値が1.0以上の因子が２つ析出された。バリマックス回転後の第１成分→因子の合計→固有値は1.883、分散の説明率は31.375%、第２成分→因子の合計→固有値は1.660、分散の説明率は27.667%であった。

　因子の解釈は、因子と分析に投入した変数との相関係数に相当する統計量である因子負荷量を見る(表2)。第１成分→因子に対しては、「価格」が0.780、「顧客ニーズ」が0.615、「アフターフォロー」が0.600と正の負荷を示したため、これを「市場志向」と解釈できよう。第２成分→因子に対しては、「デザイン」が0.894、「ネーミング」が0.881と正の負荷を示したため、これを「感性志向」と解釈できよう。

【作表】出力例の表1　因子分析の固有値と分散の説明率、および、表2　バリマックス回転後の因子負荷量行列をもとにした作表例を示した。 　因子分析の結果は、固有値、分散の説明率、回転を選択した場合にはバリマックス回転後の因子負荷量を表示する。表側見出しには固有値、分散の説明率、および変数ラベルを、表頭見出しには因子の番号を掲載する。

表3　商品開発を行ううえで重視している点の因子分析

	因子
	1	2
固有値	1.883	1.660
分散の説明率	31.375	27.667
価格	.780	.042
デザイン	.104	.894
ネーミング	.132	.881
顧客ニーズ	.615	.111
費用	.713	.024
アフターフォロー	.600	.266

※表中の統計量は、主因子解によるバリマックス回転後の因子負荷量

【出力例2：2011年度　設問21　インターネットに接続するとき使用する機械の因子分析】
　図5　[因子分析:記述統計]ダイアログ・ボックスで[1変量の記述統計量]をチェックしたため、表1が出力される。インターネットに接続するとき「パソコン」を使用するという回答は、【多重回答の度数分布表】(へ)では75.6%であったが、表4の平均値は0.7557と小数点以下4桁まで出力される。

表4　因子分析のオプションの記述統計量(21版) 記述統計量   平均値 標準偏差 分析 N パソコン .7557 .43067 221 スマートフォン .5023 .50113 221 携帯電話 .3439 .47608 221 タブレット端末（iPadやGALAXY Tab等） .0407 .19810 221 インターネットには接続していない .0226 .14904 221

　図5　[因子分析:記述統計]ダイアログ・ボックスで相関行列の[係数]をチェックしたため、表2が出力される。表2の相関係数を見ると、「インターネットには接続していない」は、「スマートフォン」(-0.153)および「携帯電話」(-0.110)よりも「パソコン」と-0.268と負の相関関係が強かったため、「パソコン」と同じ第２因子への負荷が強くなったと考えられる。(表4)。また、「スマートフォン」と「携帯電話」とは-0.537とやや強い負の相関関係を示したため、第１因子に対して「スマートフォン」は負の、「携帯電話」は正の負荷を示したと考えられる。

　デフォルトの出力である表3の説明された分散の合計は、実質的には固有値と分散の説明率である。（SPSS　22版でも）「因子」を「成分」、「固有値」を「合計」と誤表示している。図3で変更できるが、因子抽出の打ち切り基準を固有値の下限=1というデフォルトの設定で、固有値が1.0以上の因子が２つ析出された。バリマックス回転後の第１成分→因子の合計→固有値は1.571、分散の説明率は31.423%、第２成分→因子の合計→固有値は1.288、分散の説明率は25.759であった。

　因子の解釈は、因子と分析に投入した変数との相関係数に相当する統計量である因子負荷量を見る。第１成分→因子に対しては、「スマートフォン」が-0.897と負の、「携帯電話」が0.821と正の負荷を示したため、第１因子は「ケータイ」とでも解釈できよう。第２成分→因子に対しては、「パソコン」が0.737と正の、「インターネットには接続していない」が-0.844と負の負荷を示したため、第２因子は「パソコンでのネット接続」とでも解釈できよう。

【作表】出力例の表6　因子分析の固有値と分散の説明率、および、表7　バリマックス回転後の因子負荷量行列をもとにした作表例を示した。
　因子分析の結果は、固有値、分散の説明率、回転を選択した場合にはバリマックス回転後の因子負荷量を表示する。表側見出しには固有値、分散の説明率、および変数ラベルを、表頭見出しには因子の番号を掲載する。

表8　インターネットに接続するとき使用する機械の因子分析

	因子
	1	2
固有値	1.571	1.288
分散の説明率	31.423	25.759
パソコン	.207	.737
スマートフォン	-.897	.027
携帯電話	.821	.176
タブレット端末（iPadやGALAXY Tab等）	-.138	.012
インターネットには接続していない	.175	-.844

※表中の統計量は、主因子解によるバリマックス回転後の因子負荷量