 |
 |
| 22版 | 15版 |
|---|---|
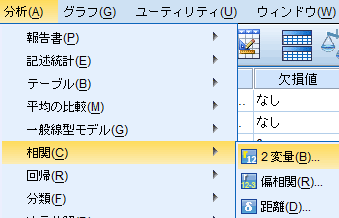
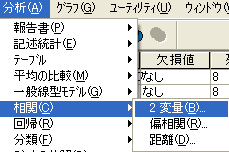
| 図1 [相関]→[2変量]の選択 | |
交差的時間差相関分析 (CORRELATIONS)
【用途】交差的時間差相関分析(cross-lagged correlation analysis)とは、2変数間の因果関係的な時間的順序を調べることを目的とする技法であり、同一のケースから少なくとも2時点から継起的なデータを収集できたパネル・データを必要とする。この技法は、ある変数xとyとの時間的順序は、先行するデータ収集時点をt1、その後に続く時点をt2とした場合、もし、t1xとt2yとの交差的相関が、t1xとt1y、および、t2xとt2yという横断的相関よりも強く、かつ、t1yとt2xとの交差的相関がこれらの横断的相関よりも弱い、という条件が成立する場合に、xはyに時間的に先行し、少なくとも、当該の2変数以外の影響を除去した場合には、xが原因でyがその結果であるという因果関係が認められる、と判断する技法である。
SPSSでの統計手続は図1のように2変量の相関分析(CORRELATIONS)である。
【データ】ここでは、PID調査【を開く】の「パネル・サンプル」から、小木曽(1987:73の図2)、小木曽(1997:217)の図3、小木曽(2007:112の図6-1,116の図6-3,136の図7-1,137の図7-2)に示した交差的時間差相関分析の例を示す。(なお、小木曽(1987:73)の図2、小木曽(1997:217)の図3と小木曽(2007:137)の図7-2は同一の図であり、これを3つの表に分割したものが小木曽(2007:112の図6-1,116の図6-2,136の図7-1)である。)
【手順】
 |
 |
| 22版 | 15版 |
|---|---|
| 図1 [相関]→[2変量]の選択 | |
以下、交差的時間差相関分析の3つの例の、[2変量の相関分析]ダイアログ・ボックス(上段)、結果の解釈(中段)、出力例(下段左)、出力にもとづく図(下段右)を示す。なお、γの小数点以下の桁数は、表は(SPSSの出力のまま)3桁、図は小数点を省略して2桁とした。
【例1:自律性と仕事への支持の交差的時間差相関分析】
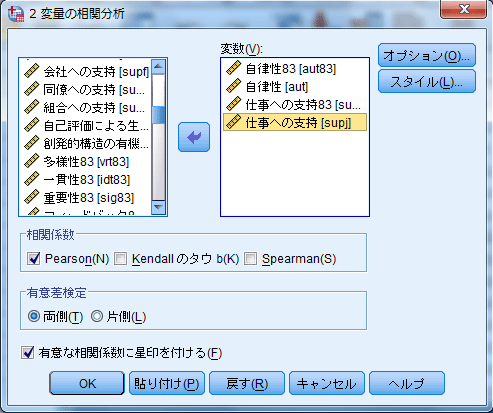
図2 表1 自律性と仕事への支持の交差的時間差相関分析(γ)を計算する[2変量の相関分析]ダイアログ・ボックス
1983年度の自律性と1984年度の仕事への支持との交差的相関が 0.804と、1983年度の自律性と仕事への支持との横断的相関の 0.661、1984年度の自律性と仕事への支持との横断的相関の 0.778よりも強く、1983年度の仕事への支持と1984年度の自律性との交差的相関が 0.551と逆の交差的相関よりも弱いことから、自律性は仕事への支持を増加させる、と判断できよう(表1,図3)。
|
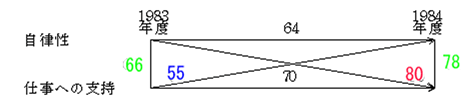 図3 自律性と仕事への支持の交差的時間差相関分析(γ) ※実質的には表1のγを小数点以下2桁で四捨五入して作図したもので、初出は小木曽(1987:73)の図2で、これを小木曽(1997:217)の図3と小木曽(2007:116)の図6-2に再録した。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
【例2:仕事への支持と会社への支持の交差的時間差相関分析】
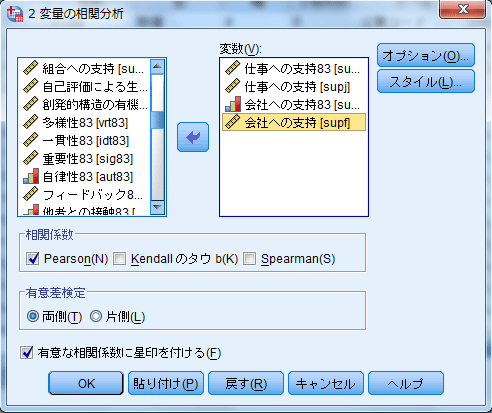
図4 表2 仕事への支持と会社への支持の交差的時間差相関分析(γ)を計算する[2変量の相関分析]ダイアログ・ボックス
1983年度の仕事への支持と1984年度の会社への支持との交差的相関が0.637と、1983年度の仕事への支持と会社への支持との横断的相関の 0.777よりも弱いが、1984年度の仕事への支持と会社への支持との横断的相関の 0.591よりも強く、1983年度の会社への支持と1984年度の仕事への支持との交差的相関が 0.389ともっとも弱いことから、仕事への支持は組織への支持を増加させる、と判断できよう(表2,図5)。
|
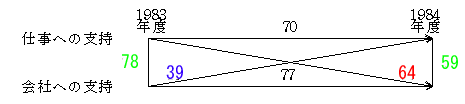 図5 仕事への支持と会社への支持の交差的時間差相関分析(γ) ※実質的には表2のγを小数点以下2桁で四捨五入して作図したもので、初出は小木曽(1987:73)の図2で、これを小木曽(1997:217)の図3と小木曽(2007:112)の図6-1に再録した。 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
【例3:会社への支持と相互評価による生産性の交差的時間差相関分析】
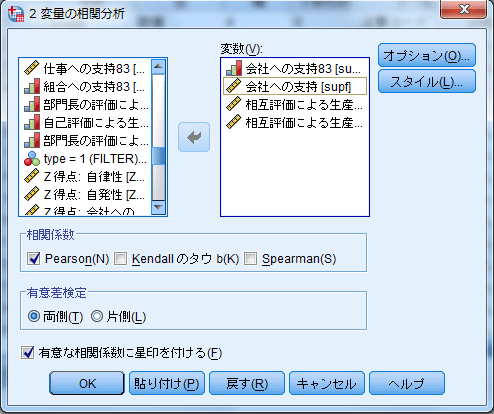
図6 表3 会社への支持と相互評価による生産性の交差的時間差相関分析(γ)を計算する[2変量の相関分析]ダイアログ・ボックス
1983年度の会社への支持と1984年度の相互評価による生産性との交差的相関が 0.617と、1983年度の会社への支持と相互評価による生産性との横断的相関の 0.609、1984年度の会社への支持と相互評価による生産性との横断的相関の 0.477よりも強く、1983年度の相互評価による生産性と1984年度の会社への支持との交差的相関が0.387ともっとも弱いことから、会社への支持は相互評価による生産性を増加させる、会社への支持は相互評価による生産性の原因となる、と判断できよう(表3,図7)。
|
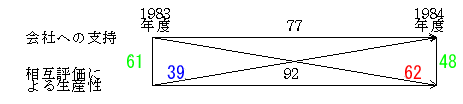 図7 会社への支持と相互評価による生産性の交差的時間差相関分析(γ) ※実質的には表3のγを小数点以下2桁で四捨五入して作図したもので、初出は小木曽(1987:73)の図2で、これを小木曽(1997:217)の図3と小木曽(2007:136)の図7-1に再録した。 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
【文献】