【目次|SPSSの使い方】へ

度数分布（単純集計） (FREQUENCIES)

【用途】度数分布は量的変数の単純集計であるが、量的変数の場合でも集計することが多い。つまり、データ入力が終了したら、まず、全変数の度数分布をとることが多い。

【データ】ここでは、國學院大学　経済ネットワーキング学科「社会経済調査ⅡA･B」1999年度「企業の環境対策への取り組みと商品開発戦略についての調査」 【を開く】の問20【を開く】の度数分布を示す。

【手順】(SPSS23-29版でもほぼ同一)

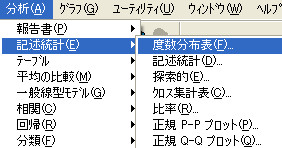
1. メニューバーの［分析］を選択し、ドロップダウン・リストから[記述統計]を、その右のドロップダウン・リストから[度数分布表]を選択する。

   29版	15版
   図1　[記述統計]→[度数分布表]の選択

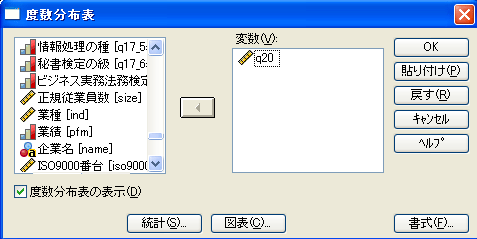
2. [度数分布表](SPSS24版では[度数])ダイアログ・ボックスで、(1)左側の変数リストから集計対象とする変数をクリックし、(2)右向き（この図では変数を選択した後なので三角形は左向きになっている）の三角形のボタンをクリックすると、(3)右側の変数ボックスに表示される。デフォルトの統計量・レイアウトでよければ、[OK]ボタンをクリックする。
   ※複数の変数を一度に選択したい時には、集計する最初の変数を左クリックし、スクロールバーを使用するなどの方法で移動し、集計する最後の変数をシフトキーを押しながら左クリックして選択する（他の統計手続でも同様）。
   もしも、集計する必要がない変数を右側の変数ボックスに選択してしまった場合には、その変数をクリックして、左向きになった三角形のボタンをクリックすると左側の変数リストに戻り集計対象から除外される。

   28版	15版
   図2　[度数分布表]ダイアログ・ボックス

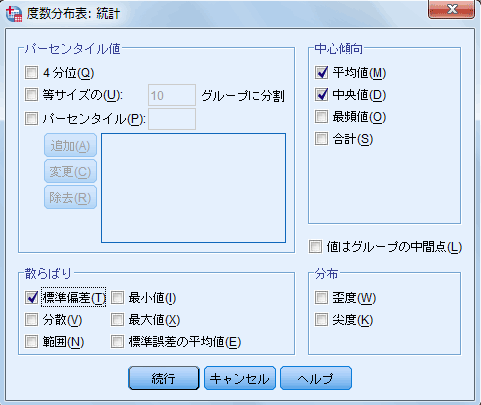
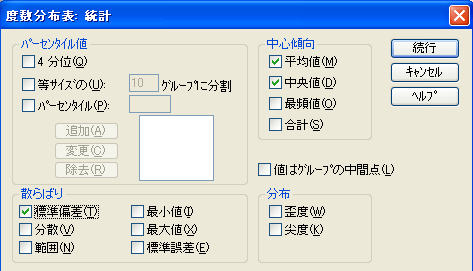
3. 平均、標準偏差、中央値、最頻値などの統計量が必要な時には、［統計ボタン］をクリックし、開かれた［度数分布表：統計]チェックボックスの必要な統計量（この例では、平均値、中央値、標準偏差）の項目をクリックし、[続行]ボタンをクリックする。

   22版	15版
   図3　[度数分布表：統計]チェック・ボックス

【デフォルトの出力】度数分布の標準出力統計量は、（左側から）変数値（指定があれば変数値ラベル）、度数、パーセント(=欠損値を分母に含む相対度数)、有効パーセント(=欠損値を分母から除去した修正相対度数)、累積パーセント(=累積修正相対度数)である。

【出力例】
　表1 は欠損値、変数・変数値ラベルを定義していない「悪い例」である。表1 の１行目には、変数ラベルを定義していないため、変数名「q20」が表示される。左から１列目は無回答を欠損値として指定していないため、すべての変数値が「有効」となる。２列目には、変数値ラベルを定義していないため、変数値「1.00」～「9.00」が表示される。３列目には「度数」、４列目には「パーセント」、５列目には「有効パーセント」、６列目には「累積パーセント」が表示される。表1 では「無回答=9」を欠損値定義していないため、「パーセント」と「有効パーセント」とが等しくなる。

表1　欠損値、変数・変数値ラベルを定義していない度数分布表の出力例(21版)

　表2 は欠損値を定義していない「悪い例」である。表2 の１行目には、シンタックス例の表4【を開く】１行目のように変数ラベルを定義したため、変数ラベル「業績」が表示される。左から１列目は無回答を欠損値定義していないため、すべての変数値が「有効」となる。２列目には、変数値ラベルを定義したため、変数値ラベルが表示されてわかりやすい表となった。３列目には「度数」、４列目には「パーセント」、５列目には「有効パーセント」、６列目には「累積パーセント」が表示される。表2 では「無回答=9」を欠損値定義していないため、パーセントと有効パーセントとが等しくなる。

表2　変数・変数値ラベルを定義したが、欠損値を定義していない度数分布表の出力例(21版)

　表3 は欠損値および変数・変数値ラベルを定義した「良い例」である。表3 の１行目には、変数ラベルを定義したため、変数ラベル「業績」が表示される。左から１列目は無回答(=9)をシンタックス例【を開く】のように欠損値定義したため、無回答を除く変数値だけが「有効」となる。２列目には、変数値ラベルを定義したため、変数値ラベルが表示されてわかりやすい表となった。３列目には「度数」、４列目には「パーセント」(=欠損値を分母に含む相対度数)、５列目には「有効パーセント」(=欠損値を分母から除去した修正相対度数)、６列目には「累積パーセント」(=欠損値を分母から除去した累積相対度数)が表示される。統計量２行目の「好調である」という回答は40人であるため、３列目の「度数」には「40」、４列目の「パーセント」(=欠損値を分母に含む相対度数)には「18.2」=(40/220)*100、５列目の「有効パーセント」(=欠損値を分母から除去した修正相対度数)には「18.5」=(40/(220-4))*100、６列目の「累積パーセント」(=欠損値を分母から除去した累積相対度数)には「19.9」=1.4+18.5、という統計量が表示される。

表3　欠損値、変数・変数値ラベルを定義した度数分布表の出力例(21版)

　 表4 は図3　[度数分布表：統計]チェック・ボックス　で指定した平均値、中央値、標準偏差の出力である。

表4　度数分布表の追加統計として平均値、中央値、標準偏差を指定した出力例