【目次|SPSSの使い方】へ

回帰分析 (REGRESSION)

【用途】回帰分析【を開く】は、量的な（順序尺度を含む）変数について、複数の独立変数によって１つの従属変数を説明する際に用いる。

【データ】ここでは、PID調査【を開く】の「工業デザイン・サンプル」から、従属変数が相互評価による生産性、独立変数が自律性、自発性、仕事への支持、会社への支持、および、組合への動員、とする回帰分析の例を示す。【相関分析】(へ)

【手順】

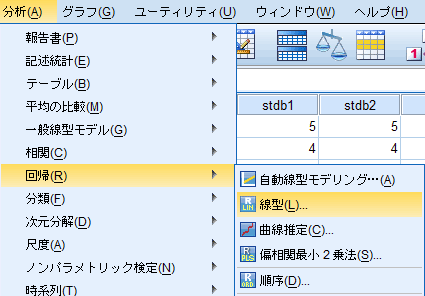
1. メニューバーの［分析］を選択し、ドロップダウン・リストから[回帰]を、その右のドロップダウン・リストから通常は[線型]を選択する(図1)。

   22版	15版
   図1　[回帰分析]→[線形回帰]の選択

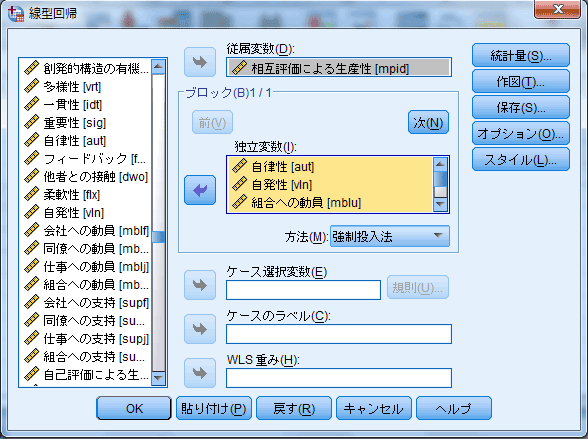
2. [線型回帰]ダイアログ・ボックス(図2)で、左側のリストから従属変数を選択し、
3. 上側の従属変数ボックスの左の右向きの16版以降ならば矢印、15版以前ならば三角形のボタンをクリックすると、その右側の従属変数ボックスに表示される。
4. 左側のリストから独立変数を選択し、
5. 上から二番目の独立変数ボックスの左の右向きの（この図では変数を選択した後なので左向きになっている）16版以降ならば矢印、15版以前ならば三角形のボタンをクリックすると、その右側の独立変数ボックスに表示される。
6. 独立変数を一括して回帰式に投入する強制投入法、デフォルトの計算方法・統計量、リスト単位での欠損値の除去でければ、[OK]ボタンをクリックする。

   22版	15版
   図2　[線形回帰](強制投入法)ダイアログ・ボックス

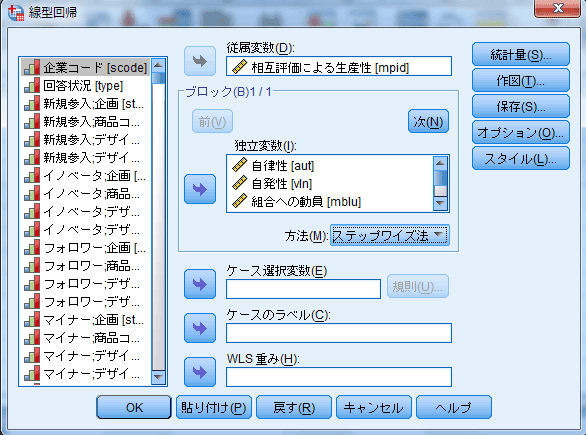
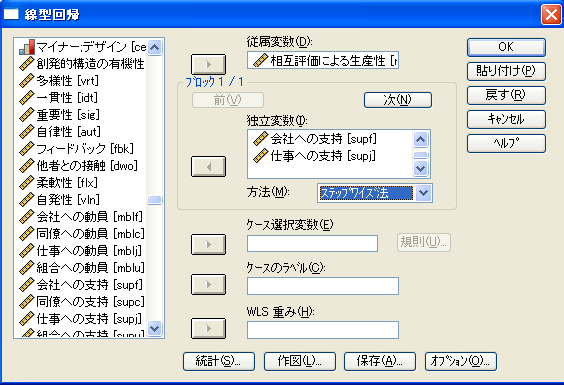
7. 独立変数を(デフォルトではt検定が有意な順から)ひとつずつ回帰式に投入するステップワイズ法(逐次投入法)を選択する場合には、独立変数ボックスの下の[方法]ドロップダウン・リストから[ステップワイズ法]を選択し、デフォルトの計算方法・統計量、リスト単位での欠損値の除去でければ、[OK]ボタンをクリックする。

   22版	15版
   図3　[線形回帰](ステップワイズ法)ダイアログ・ボックス

【デフォルトの出力】標準出力統計量は表ごとに、まず、回帰式について、投入済み変数または除去された変数、モデル集計（重相関係数(R)、決定係数(R2 乗)、調整済み R2、乗推定値の標準誤差）、分散分析（平方和、自由度、平均平方、Ｆ値、有意確率）、個々の独立変数についての係数（非標準化係数の回帰係数(B)と標準誤差、標準化係数(β:ベータ)、ｔ値、有意確率）である。
　デフォルトではリスト単位で欠損値除去される。

【出力例1：強制投入法による線形回帰】従属変数が相互評価による生産性、独立変数が自律性、自発性、仕事への支持、会社への支持、および、組合への動員、とする回帰分析
　相互評価による生産性を従属変数として、自律性、自発性、仕事への支持、会社への支持、および、組合への動員を強制投入した結果、R(重相関係数)は0.566、R2乗(決定係数)は0.320であった(表1)。

表1　強制投入法による線形回帰のモデル要約(21版) モデル要約 モデル R R2 乗 調整済み R2 乗 推定値の標準誤差 1 .566a .320 .250 .39204 a. 予測値: (定数)、仕事への支持, 組合への動員, 自律性, 会社への支持, 自発性。

　Ｆ検定の分散分析の有意確率は0.002で、1%水準で有意であった(表2)。

　個々の変数の説明力の強さを示すベータ(β)とそのt検定の有意確率(以下、「P=」と略す)は、自律性(β=-0.078、P=0.615)、自発性(β=-0.158、P=0.326)、組合への動員(β=-0.427、P=0.002)、会社への支持(β=0.490、P=0.002)、仕事への支持(β=0.170、P=0.352)であった(表3)。つまり、会社への支持と組合への動員は相互評価による生産性を1%水準で有意に説明することができた。しかし、自律性、自発性、および、仕事への支持はいずれも相互評価による生産性を有意に説明することができなかった。このように、強制投入法による線形回帰の場合では、統計的に有意な説明力がない独立変数も回帰式に投入される。【偏相関分析】(へ)

【出力例2：ステップワイズ法による線形回帰】デフォルトのβの有意水準が5%以下であることを変数投入の打ち切り基準としたステップワイズ法による、従属変数が相互評価による生産性、独立変数が自律性、自発性、仕事への支持、会社への支持、および、組合への動員、とする回帰分析を行った。
　その結果、モデル2、すなわち、２つの独立変数を投入した段階で変数投入が打ち切られ、R(重相関係数)は0.545、R2乗(決定係数)は0.297であった(表4)。

表4　ステップワイズ法による線形回帰のモデル要約(21版) モデル要約 モデル R R2 乗 調整済み R2 乗 推定値の標準誤差 1 .390a .152 .136 .42076 2 .545b .297 .269 .38693 a. 予測値: (定数)、会社への支持。 b. 予測値: (定数)、会社への支持, 組合への動員。

　モデル2の、会社への支持と組合への動員の２変数を投入した回帰式の分散分析のF検定の有意確率は0.000と1%水準で有意であった(表5)。

　相互評価による生産性をベータのt検定の有意水準が5%以下で説明することができたのは、会社への支持(β=0.486、P=0.000)と組合への動員(β=-0.392、P=0.002)だけであった(表6)。【偏相関分析】(へ)

　自律性(β=-0.084、P=0.532)、自発性(β=-0.108、P=0.396)、および、仕事への支持(β=0.034、P=0.815)は、これらを回帰式に投入したとしてもベータのt検定の有意水準が5%以上であり、相互評価による生産性を有意に説明することができなかった(表7)。【偏相関分析】(へ)