 |
 |
| 22版 | 15版 |
|---|---|
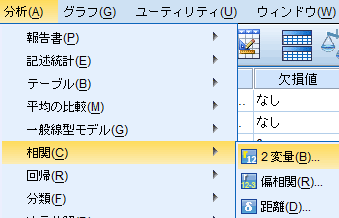
| 図1 [相関]→[2変量]の選択 | |
 |
 |
| 22版 | 15版 |
|---|---|
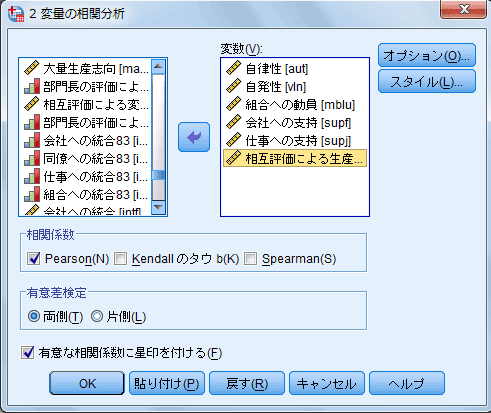
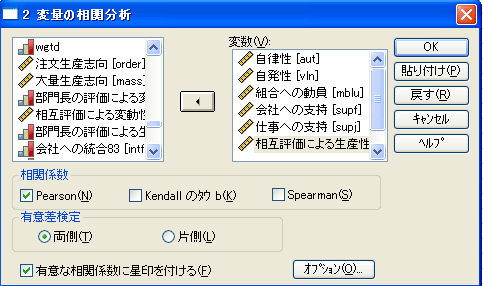
| 図2 [2変量の相関分析]ダイアログ・ボックス | |
相関分析 (CORRELATIONS)
【用途】相関分析【を開く】は量的な(順序尺度を含む)2変数間の関係を分析し、Peasonの(積率)相関係数(γ)などを計算する際に用いる。1.尺度構成など説明変数と被説明変数との区別がない分析(へ)の予備のためにも、2.説明変数と被説明変数との区別がある因果分析(へ)の予備のためにも用いることができる。
【データ】ここでは、PID調査【を開く】の「工業デザイン・サンプル」から、(回帰分析の例で用いる)自律性、自発性、仕事への支持、会社への支持、組合への動員、および、相互評価による生産性の相関分析を示す。
【手順】
 |
 |
| 22版 | 15版 |
|---|---|
| 図1 [相関]→[2変量]の選択 | |
 |
 |
| 22版 | 15版 |
|---|---|
| 図2 [2変量の相関分析]ダイアログ・ボックス | |
【デフォルトの出力】各変数のペアのセルごとの標準出力統計量は、(上から)Peasonの(積率)相関係数(γ)【を開く】、(小数点以上を省略した小数点以下3桁)、両側検定の有意確率【を開く】、有効ケース数(N)である。
デフォルトではペア単位で欠損値除去される。
【出力例】
対角要素である自律性どおしのペアのセルには「1」が表示される。自律性と自発性とのペアに着目すると、セルの上から、Pearson の相関係数が.533(=0.533)とやや強い正の相関関係、有意確率 (両側)が.000と1%水準で有意であり、N(=有効ケース数)が57である。
相互評価による生産性との相関に着目すると(表1)、自律性は0.140と無相関、自発性は0.042と無相関、組合への動員は-0.273とやや弱い負の相関関係、会社への支持は0.397(≒0.40)とやや強い正の相関関係、仕事への支持は0.183と無相関であった。【回帰分析】(へ)でともに相互評価による生産性との相関を有意に説明することができた会社への支持と組合への動員とは0.262とやや弱い正の相関関係にあった。【偏相関分析】(へ)
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
【作表】正方行列の相関行列、すなわちある変数群のすべての組み合わせの相関係数を表示する場合は、相関係数γは、小数点以上(つまり0)を省略して、少数点以下3ケタまで、相関行列の左下半分を表示し、重複する右上半分は省略し、対各要素は省略する(ので表頭の変数番号は1つ少なくなる)。表側に番号をつけた変数ラベルを表記し、表頭には変数の番号だけを記載することが多い。なお、相関係数γの有意水準が5%以下であれば係数の右に* (アスタリスクを1つ)、1%以下であれば係数の右に**(同2つ)表記することもある。
SPSSの[相関][2変量]の出力では、慣習では行を起こして作表しない両側検定の有意水準(確率)と有効ケース数の各行が出力されるため、エクセルへの張り付けを行う場合には、因子分析などの統計量を用いた方が楽かもしれないが、この場合は欠損値除去をペア単位とするのかリスト単位とするのか注意すること。表2は、因子分析の[記述統計]によってペア単位で欠損値除去した相関行列をもとに作表した例である。なお、量的変数の「基礎統計量」として、相関行列に有効ケース数、平均値、標準偏差を付加した表を作成することが多い。
| 有効ケース数 | 平均値 | 標準偏差 | 相関係数(γ) | |||||
|---|---|---|---|---|---|---|---|---|
| 1) | 2) | 3) | 4) | 5) | ||||
| 1)自律性 | 57 | 3.60 | 0.32 | |||||
| 2)自発性 | 57 | 3.84 | 0.21 | .533 | ||||
| 3)組合への動員 | 55 | 2.55 | 0.35 | -.048 | .062 | |||
| 4)会社への支持 | 57 | 2.70 | 0.31 | .402 | .336 | .262 | ||
| 5)仕事への支持 | 57 | 3.28 | 0.24 | .524 | .606 | .256 | .566 | |
| 6)相互評価による生産性 | 67 | 3.29 | 0.43 | .140 | .042 | -.273 | .397 | .183 |