 |
 |
| 22版 | 15版 |
|---|---|
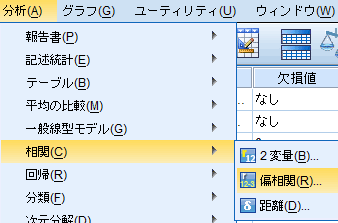
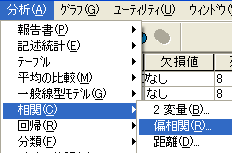
| 図1 [相関]→[偏相関]の選択 | |
 |
 |
| 22版 | 15版 |
|---|---|
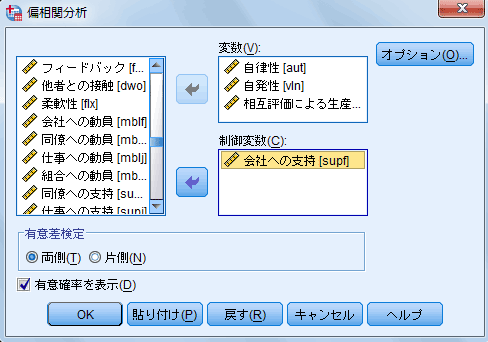
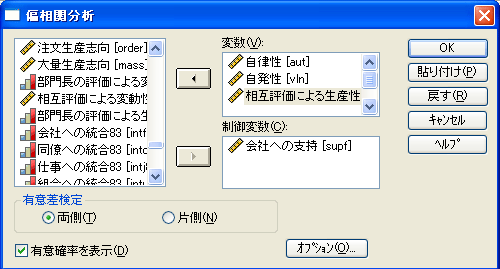
| 図2 [偏相関分析]ダイアログ・ボックス | |
偏相関分析 (PARTIAL CORR)
【用途】偏相関分析【を開く】は、量的な(順序尺度を含む)変数について、ある変数を統制した(統制変数の影響を除去した)場合の2変数間の関係を分析する際に用いる。統制変数を第3変数と呼ぶこともある。
【データ】ここでは、PID調査【を開く】の「工業デザイン・サンプル」から、(回帰分析の例で用いる)自律性、自発性、仕事への支持、会社への支持、組合への動員、および、相互評価による生産性の相関分析を示す。【相関分析】(へ)|【回帰分析】(へ)
【手順】
 |
 |
| 22版 | 15版 |
|---|---|
| 図1 [相関]→[偏相関]の選択 | |
 |
 |
| 22版 | 15版 |
|---|---|
| 図2 [偏相関分析]ダイアログ・ボックス | |
【デフォルトの出力】各変数のペアごとの標準出力統計量は、(上から)偏相関係数(小数点以上を省略した小数点以下3桁)、両側検定の有意水準、自由度である。
デフォルトではリスト単位で欠損値除去される。
【出力例1:原因となるだろう変数を統制して相関を確認する例】【回帰分析】(へ)の結果では、相互評価による生産性を有意に説明することができた会社への支持を統制変数(=制御変数)とした場合に、自律性および自発性と相互評価による生産性との偏相関を分析した結果(表1)、会社への支持を統制した相互評価による生産性との偏相関係数は、自律性が-0.032、自発性が-0.111といずも無相関であった。
| ||||||||||||||||||||||||||||||||||||||||||||||||||||
【出力例2:第3変数を統制することにより相関が強まる例】2変量の【相関分析】(へ)の結果、-0.273というやや弱い負の相関関係にあった)会社への動員と相互評価による生産性との偏相関係数は、会社への支持を統制した場合には-0.413と(小木曽(1997:201参照、ただし同頁後から5行目には-0.25と入力ミス【を開く】していることがこのマニュアルの作成時に発覚した。だいたい単相関で-0.27なのに偏相関で-0.25であったら、ここの文章は矛盾している。-0.413が正しい偏相関係数の値である。)とやや強い負の相関関係となる。つまり、組合への動員と正の相関関係にある会社への支持の影響を除去することによって、組合への動員と相互評価による生産性との負の相関関係がより強まった。【回帰分析】(へ)
| |||||||||||||||||||||||||||||||